Lenny is an artist, designer, polymath, and neographer. Understanding how to design unique numerical notations has encouraged Lenny to jump around disciplines and as a result he has a basic understanding of many fields of study. He finds that systems, in general, are easy to grasp when immersed in them for a while and they all seem interconnected in some way or another. He thoroughly enjoys discovering these connections.
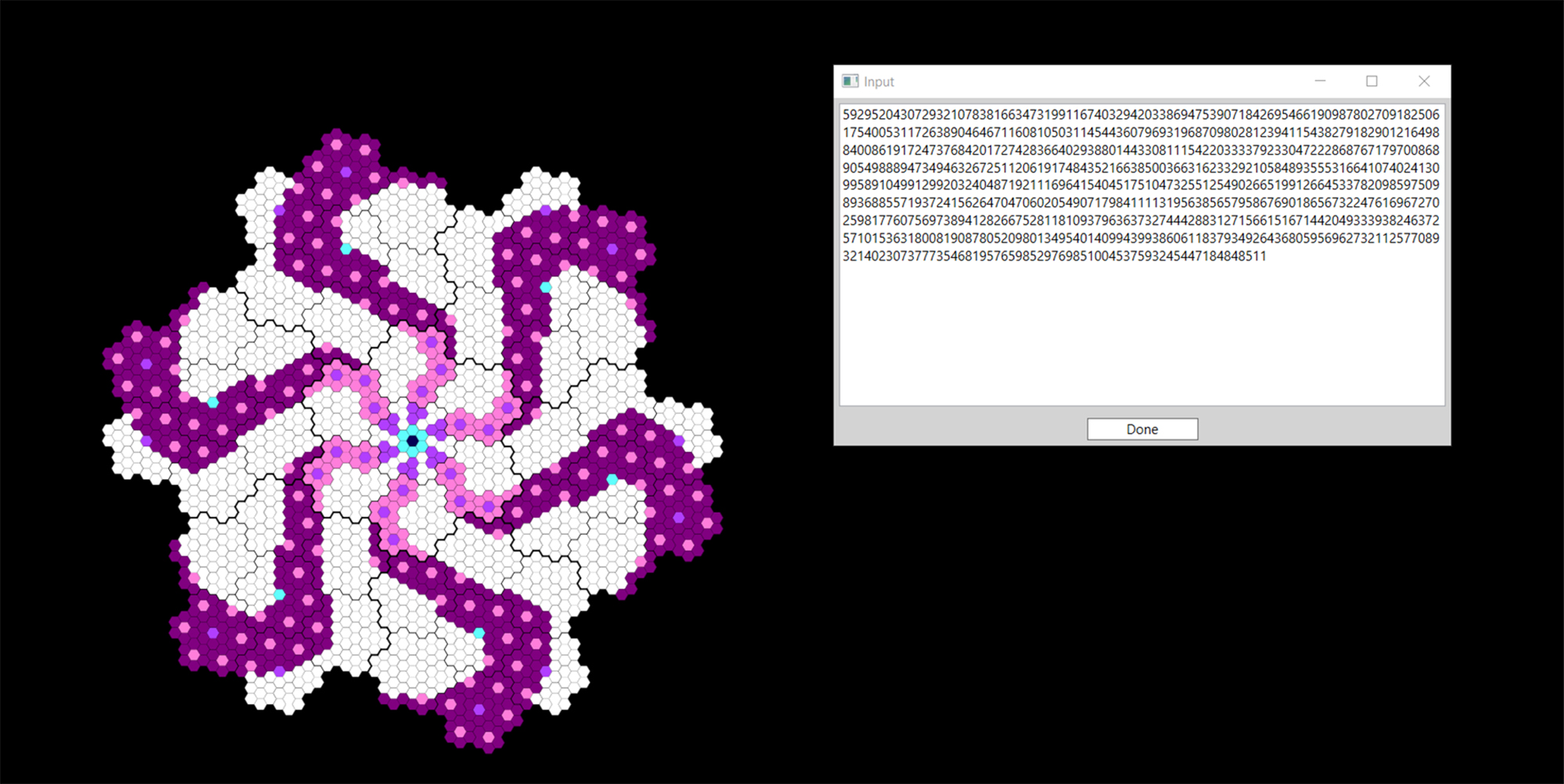
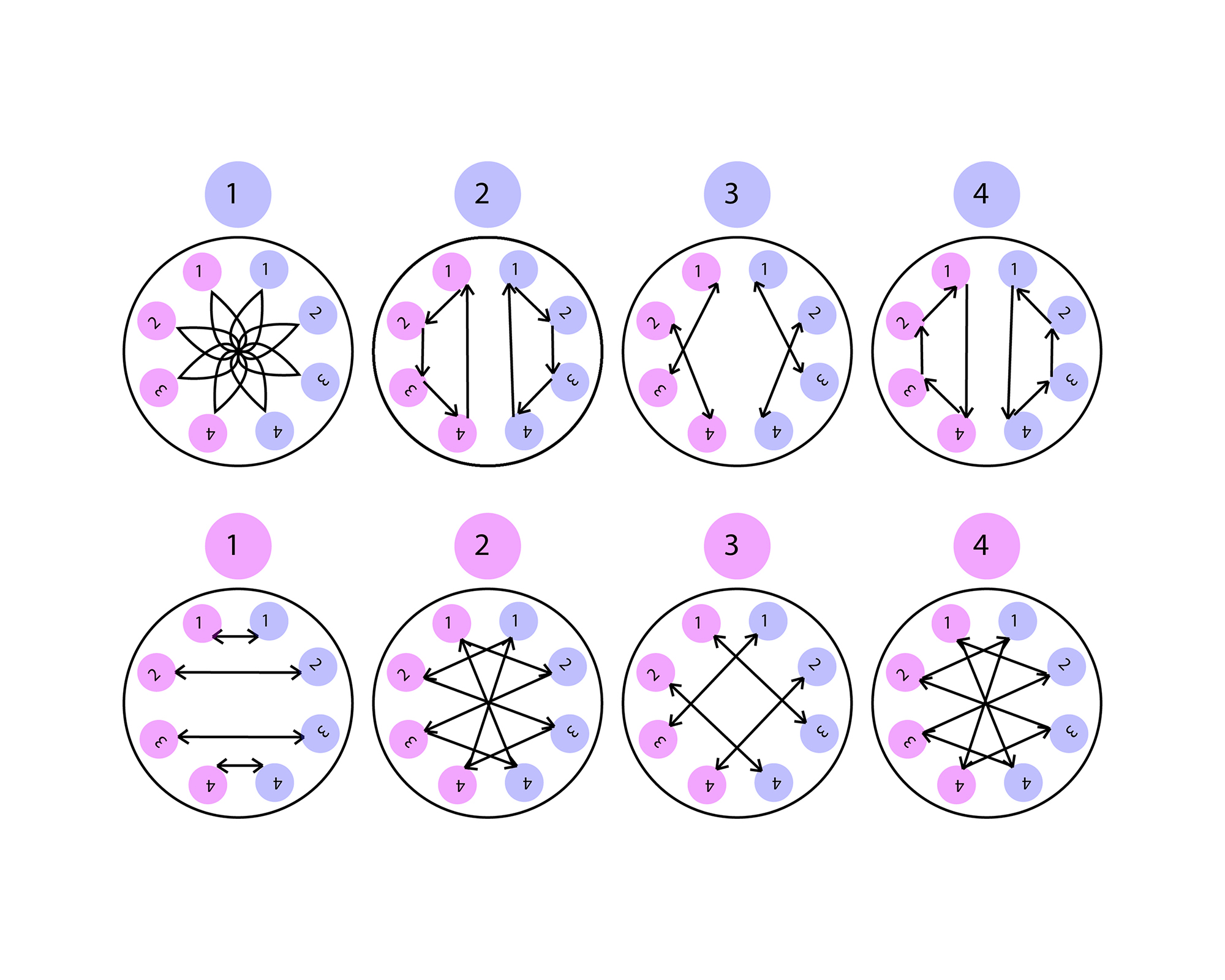
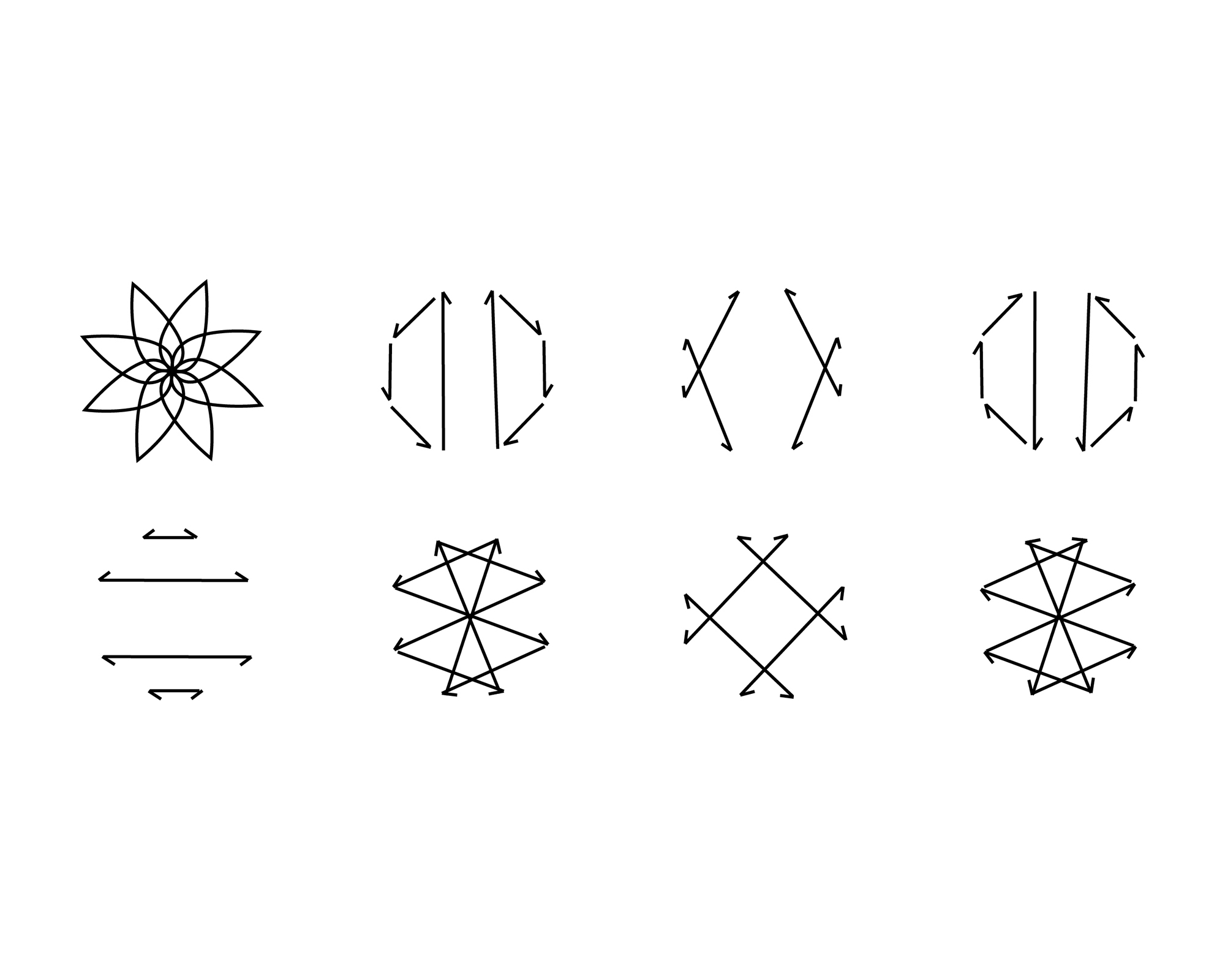
Lenny plays in the margins of number theory, systems theory, pattern recognition, data visualization, language creation, and art/design. While designing new notational systems for numbers he creates graphs, tables, diagrams and objects as tools for researching number relationships but also as artworks. Most of his numerical notation utilizes spatiality and positionality more than linear number notation. The aesthetics of symmetry is often a recurring element when working with numbers and can be seen in most of his work.
The following questions are constantly motivating Lenny to research and experiment with numbers and notation.
– Why has most of the world settled on a universal language of base 10 for most mathematical based operations? Would it be beneficial to have a diverse collection of mathematical languages for solving specialized mathematical problems?
– How can reading direction change our understanding of a number? For instance, instead of left to right, what might spiral reading look like?
– What happens when a person begins thinking and talking with a new language for numbers?
– How can we use art and design principles to aesthetically build notational languages for numbers?
– How do other animals perceive and communicate concepts like distance, time, and other measurement reliant phenomena? Can we learn their ways of understanding these concepts? Could they have number systems we might be able to learn?
– What might mathematical symbols for extraterrestrial intelligences look like?
– If intelligent life evolved from a galaxy made of both antimatter and matter would their early understanding of negative numbers be different than ours?
– What other signs besides negative and positive can exist in number systems and how might they function?
– What does a number ribbon look like? (partially 2 dimensional number line)
– How can we build 4 dimensional notation for numbers?